In "Surely You're Joking, Mr. Feynman!" Feynman recounts how he enj...
The author is referring to the Forgetting Curve, or the Ebbinghaus ...
Laurie Brown studied at Cornell University, where in 1951 he receiv...
In one interview Feynman described his method for reading scientifi...
Here's a photo of Feynman's last blackboard at Caltech
, I
want to comment on some of the vicissi-
tudes I have experienced while being
taught physics.
The basic courses of my first two
years were disappointing. They didn’t
really give me the opportunity to join
that greatest adventure. Most of my
l e c t u r e r s f o l l o w e d t r a d i t i o n a l t e a c h i n g
a p p r o a c h e s b a s e d h e a v i l y o n s o l v i n g
standard problems and learning by rote,
with no hint of free inquiry or discus-
sion. They seemed to be convinced that
we would understand physics through
that method. I was not enthusiastic.
Traditional teaching
My fellow students and I spent a lot of
time and effort solving textbook-style
problems. But we didn’t really under-
stand physics by doing that. In practice,
we were mostly trained to use problem-
solving techniques. Feynman touched
on that failing when he said, “I don’t
know what’s the ma#er with people:
they don’t learn by understanding;
they learn by some other way—by rote
or something. Their knowledge is so
fragile!”
2
I felt that fragility. The time crunch of
a heavy course load forced me to mem-
orize a lot of equations and mathematical
procedures in order to pass my physics
exams.
As time passed, I forgot many of the
things I had studied. Noam Chomsky,
i n t e r v i e w e d i n 2 0 1 2 f o r t h e L e a r n i n g
Without Frontiers Conference, put it best
when he said,
A person can do magnificently on
a test and understand very li#le.
We’ve all had the experience of
“acing a test” and forge#ing
everything two weeks later....
Passing tests doesn’t begin to
compare with inquiring, search-
ing, pursuing topics that engage
us and excite us. In fact, you
will remember what you dis-
cover—if you pursue this kind of
learning.
The aspects of physics I have under-
stood best so far are those I have studied
for pleasure. I understood special rela-
tivity be#er when I derived the Lorentz
transformations in a different form.
3
This
task was much more exciting than the
usual assignment of calculating the
length contraction of a rod. I understood
Maxwell’s equations be#er when I re-
viewed the Helmholtz theorem
4
and this
task was far more thrilling than calculat-
ing the electric field of a charged sphere.
Traditional teaching methods urge us
to perform standard calculations that
rarely spark our creativity. Being im-
mersed in such teaching, I feel trapped in
a labyrinth whose exit can only be found
by solving a ton of mostly uninteresting
textbook problems.
The idea that solving such problems
is not the best way to understand physics
was succinctly expressed by Dieter
Nachtigall:
Pupils can o!en solve what text-
book authors call “problems” with-
out understanding the physics
concepts involved in them. Such
“problem solving” o!en exhibits
nothing else than the ability to find
some appropriate equations, put
them together, manipulate them
algebraically, fill in figures and fi-
nally come out with the “correct
answer.” A student can be good
with the formulae but may have
understood nothing about the
physics behind them.
5
Learning by creating
A robust alternative to traditional
teaching is one that prioritizes creative
thinking. That is the approach that
Feynman strongly emphasized. Laurie
Brown, a former pupil of his, comments
that
Commentary
How to teach me physics: Tradition is not always a virtue
Tradition, discipline,
and reverence
are necessary
to learn physics.
I agree,
my students
must solve tons
of problems
to pass exams.
The traditional
curriculum is ok
by definition.
Learning by creating?
Free inquiry? Physics X?
Feynman is crazy!
TRADITIONAL PHYSICS TEACHERS teach us to swim on the surface but not in the
deep, where, as Steven Weinberg says, “the unclear, uncharted areas of science can lead
to creative work” (Nature 426, 389, 2003).
MARCH 2017
|
PHYSICS TODAY 11
Feynman stressed creativity—
which to him meant working
things out from the beginning. He
urged each of us to create his or
her own universe of ideas, so that
our products, even if only answers
to assigned classwork problems,
would have their own original
character.
6
Feynman’s way of teaching is perhaps
best described in three words: learning
by creating. As he said,
It’s the way I study—to under-
stand something by trying to work
it out or, in other words, to under-
stand something by creating it.
Not creating it one hundred per-
cent, of course; but taking a hint as
to which direction to go but not
r e m e m b e r i n g t h e d e t a i l s . T h e s e
you work out for yourself.
In a le#er to a student asking for
advice, Feynman touched again on that
point:
All you have to do is, from time to
time—in spite of everything, just
try to examine a problem in a
novel way. You won’t “stifle the
creative process” if you remember
to think from time to time. Don’t
you have time to think?
7
The problem is, however, that as stu-
dents we are o!en not given proper time
to think! We are instead overwhelmed
with solving problem sets, writing lab
r e p o r t s , a n d w o r r y i n g a b o u t p a s s i n g
exams. Remarkably, Feynman empha-
sized creativity in physics until his very
last days. He wrote on his blackboard
shortly before he died, “What I cannot
create I do not understand.”
The Feynman Lectures on Physics clearly
exhibit their author’s unconventional ap-
proach. David Goodstein (P
HYSICS TODAY,
February 1989, page 70) says of the lectures,
If his purpose in giving them was
to prepare classes of adolescent
boys to solve examination prob-
lems in physics, he may not have
succeeded particularly well. . . . If,
however, his purpose was to illus-
trate, by example, how to think
and reason about physics, then, by
all indications, he was brilliantly
successful.
Feynman’s lectures successfully omit-
ted proposed problems. His teaching
style is also exemplified in the noncredit,
no-homework, no-registration, tuition-
free Physics X course he offered at Cal-
tech. Students met weekly, and the cur-
riculum consisted of whatever they felt
like discussing. The primary focus was to
promote a culture of free inquiry and joy
toward the subject. In the lectures I have
a#ended so far at UCL, the idea of enjoy-
ing physics has not even been raised.
Feynman said,
The best teaching can be done only
when there is a direct individual
relationship between a student
and a good teacher—a situation in
which the student discusses the
ideas, thinks about the things, and
talks about the things.
1
Such teaching is mostly absent from my
current physics education.
As a student, I have not yet been able
to reconcile the traditional approach
with my firm conviction that the best
physics teaching puts a premium on cre-
ativity and free inquiry. Feynman has
shown that such creative teaching is
possible.
References
1. R. P. Feynman, R. B. Leighton, M. Sands,
The Feynman Lectures on Physics, vol. 3,
Addison-Wesley (1965).
2. R. P. Feynman, R. Leighton, “Surely You’re
Joking, Mr. Feynman!” Adventures of a
Curious Character, E. Hutchings, ed., W. W.
Norton (1985), p. 36.
3. R. Heras, Eur. J. Phys. 37, 025603 (2016);
Eur. J. Phys. 38, 019401 (2017).
4. R. Heras, Eur. J. Phys. 37, 065204 (2016).
5. D. K. Nachtigall, Eur. J. Phys. 11, 1 (1990).
6. L. M. Brown, “Most of the Good Stuff”:
Memories of Richard Feynman, L. M. Brown,
J. S. Rigden, eds., American Institute of
Physics (1993), p. 54.
7. R. P. Feynman, Perfectly Reasonable Devia-
tions from the Beaten Track: The Letters of
R. P. Feynman, M. Feynman, ed., Basic
Books (2005), p. 283.
Ricardo Heras
(ricardo.heras.13@ucl.ac.uk)
University College London
London, UK
Approaches to studying our history
LETTERS
I
share Ma# Stanley’s view that study-
ing the history of our subject enriches
our perspectives as practicing physi-
cists (“Why should physicists study
h i s t o r y ? , ” P
HYSICS TODAY, July 2016,
page 38). In my talks to the nontechnical
public and in presentations of new re-
sults to colleagues, I try to emphasize
the complex network of chance influ-
ences, mistakes, collaborations, and con-
troversies that lie behind discoveries
conventionally caricatured by a#ribut-
ing them to one person.
Stanley and I part company when he
complains about those who interpret the
science of the past in terms of what we
know today: “the bugbear of . . . Whig
history.” Of course, it is essential to
study scientific advances in the social,
economic, and cultural context of their
times, as professional historians do. But
Whig history is a complementary activ-
ity, justifiable on several grounds.
Our scientific predecessors are cele-
brated largely because of the science
that their discoveries led to; that is why
they are important, and why historians
study them. And the significance of their
science changes with time, so it is in-
evitable that we regard it differently as
we look back: With the discovery of the
Aharonov–Bohm effect, the magnetic vec-
tor potential of James Clerk Maxwell and
his Victorian contemporaries takes on a
new meaning. In addition, many of our
famous predecessors were cleverer and
wiser than us; they le! “time bombs,” ig-
nored for generations until, suddenly
triggered by resonating with a contem-
porary preoccupation, they explode.
One such time bomb is Isaac New-
ton’s query 3, which he posed
1
a!er
decades of struggling to accommodate
Grimaldi’s observation of edge diffrac-
tion fringes in his ray theory of light:
“Are not the Rays of Light, in passing by
the edges and sides of Bodies, bent sev-
eral times backwards and forwards, with
a motion like that of an Eel? And do not
the three Fringes of colour’d Light
above-mention’d arise from three such
bendings?” Now, three centuries later,
and thanks to three insights, we can un-
derstand
2
that this apparently eccentric
remark makes perfect sense.
The first insight was Sommerfeld’s
1896 exact solution of Maxwell’s equa-
tions for light diffracted by a conducting
half plane.
3
The second insight was
Braunbek and Laukien’s 1952 calculation
4
exhibiting Newton’s eel-like undulations
by plo#ing the trajectories of the Poynting
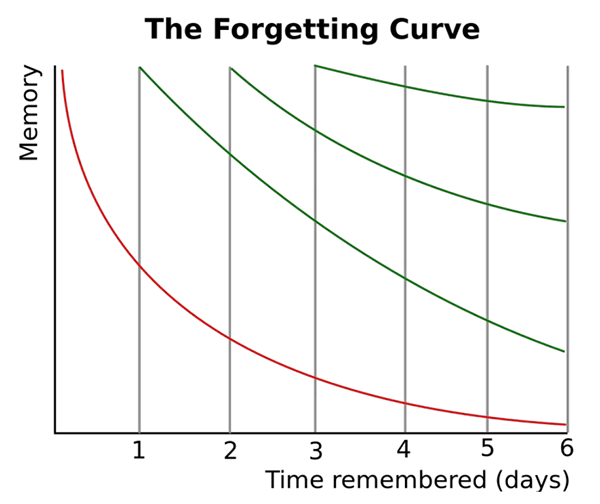
The author is referring to the Forgetting Curve, or the Ebbinghaus Curve of Forgetting, which hypothesizes the decline of memory retention in time.
This curve shows how information is lost over time when there is no attempt to retain it.
In 1885, Hermann Ebbinghaus theorized that the rate at which we forget information is influenced by various factors, including the complexity of the material learned (such as its meaningfulness), its presentation, and physiological elements like stress and sleep. He also postulated that the fundamental forgetting rate is relatively consistent among individuals. Ebbinghaus concluded that differences in memory performance can be attributed to individuals' mnemonic representation skills.
Furthermore, he suggested that basic instruction in mnemonic techniques could partially mitigate these disparities. Ebbinghaus maintained that the most effective strategies for enhancing memory retention are:
1. Improving memory representation (for example, using mnemonic techniques)
2. Employing repetition based on active recall (particularly spaced repetition).
Thank you so much for these comments, Luis. They helped bring parts of this commentary alive!
Here's a photo of Feynman's last blackboard at Caltech

Laurie Brown studied at Cornell University, where in 1951 he received his Ph.D. under Richard Feynman

In one interview Feynman described his method for reading scientific papers:
1. Read the abstract
2. Try to predict what are the results and conclusions of the paper.
3. Go to the “Conclusions” section — check whether your prediction stands.
4. If your prediction was successful don't bother reading the rest of the paper, go to the next one.
5. If the outcome surprised you, then read the whole paper and carefully study the methods.
This method emphasizes Feynman's obsession to push himself to think creatively instead of merely following another person's line of reasoning.
In "Surely You're Joking, Mr. Feynman!" Feynman recounts how he enjoyed playing pranks on people during his college years. Many of these pranks aimed to highlight people's gullibility. For instance, in an MIT mechanical drawing class where students were taught to use a drawing tool called a French curve (a curved plastic piece for sketching smooth curves), Feynman told his classmates that "at the lowest point of each curve, the tangent remains horizontal regardless of the curve's orientation." The other students, intrigued by this revelation, began examining their French curves, rotating them in different ways to confirm that the tangent was always horizontal at the lowest point. Feynman found this amusing, as these students had already studied calculus and should have known that the derivative of any curve's minimum is zero.