Particles having energies above $10^{18}$ eV are the so-called ultr...
The Cosmic Microwave Background (CMB), discovered in 1966 by A. Pen...
The main reactions causing energy losses while the CR propagation a...
We can easily determine the distance scale for energy loss given by...
As a simple exercise, one can calculate the threshold energy of pro...
Spectrum of UHECR as observed by HiRes, TA and Auger experiments (a...
Today the upper limit on the energy of Cosmic Rays is called **Grei...
VOLUME
16,
NUMBER
17
PHYSICAL
REVIEW
LETTERS
25
APRiL
1966
tons.
When
the
complete
potential
is
deformed,
the
optical
parameters (Table
I)
found
so
far
to
give
the best
fit
to the
elastic
polarization
also
produce
the best
prediction
of inelastic
asymmetry.
All
the
curves in
Fig.
2
use
a
central-well
deformation
parameter
of
P,
=0.
39 for
~si
and
P,
=
0.
22
for
~Ni.
The deformation
parameter
of the spin-orbit term
is
1.
5
times the
central-
well
value,
which
produces
slightly
better
agree-
ment with the
asymmetry
data
for
"Si.
Both
real and
imaginary
parts
of
the
spin-orbit
in-
teraction are
included,
but since
i
W~I
«VS,
the
imaginary part
makes
little difference.
The
curves
also include Coulomb-excitation
amplitudes,
'
which make little
difference in
either the
asymmetry
or
the cross section.
We
find that for
all
of the
calculations
made,
the predictions
of inelastic
asymmetry
and
inelastic
polarization are
very
nearly
identi-
cal.
In
summary
we
find
that,
provided
the
imag-
inary
and
spin-orbit terms
are included,
the
collective-model
generalization
of the
optical
potential
gives
a
good
account of the
present
inelastic
asymmetry
data at all but
the
most
forward
angles.
It
is
quite
possible
that
a
more
comprehensive
treatment of
the
spin-de-
pendent
interaction will
improve
matters in
this
region,
and
such
calculations are in
pro-
gress.
It
is a
pleasure to
acknowledge
many
useful
conversations concerning
this work with G. R.
Satchler and N.
M.
Hi.ntz. We
are much indebted
to
the
indefatigable
ORIC
cyclotron
operators,
and
to
M. B.
Marshall,
W.
H.
White,
I.
B.
Schneider,
and A. W.
Riikola of the
ORIC
staff,
for their
essential
contributions to the
experi-
mental
effort.
*Research
sponsored
by
the
U. S.Atomic
Energy
Com-
mission
under
contract
with
the Union Carbide Corpora-
tion.
)Oak Ridge
Graduate
Fellow
from
the
University
of
Minnesota under
appointment
from
Oak
Ridge
Asso-
ciated
Universities.
f.
Graduate
Fellow from the
University
of Tennessee
under
appointment
from
the National Science
Founda-
tion.
~R.
H.
Bassel, G. R. Satchler, R. M. Drisko,
and
E.
Rost, Phys.
Rev.
128,
2693
(1962).
The
present
DW
calculations include the spin-orbit
term in the
elag+ic
distortion.
M.
P. Fricke and
G.
R. Satchler,
Phys.
Rev.
139,
B567
(1965).
3T.
Stovall
and
N. M.
Hintz,
Phys.
Rev.
135,
B330
(1964).
See,
for
example, W.
S.
Gray,
R.
A.
Kenefick,
J.
J.
Kraushaar,
and
G.
R.
Satchler,
Phys.
Rev.
142,
735
(1966);
G. R.
Satchler,
to
be
published.
5E.
R.
Flynn
and
R. H.
Bassel,
Phys.
Rev.
Letters
15,
168
(1965),
and
other
references
given
there.
6L.
N.
Blumberg,
E. E.
Gross, A.
van
der
Woude,
and
A.
Zucker,
Nucl. Instr.
5
Methods
~39
125
(1966);
L.
N.
Blumberg,
E. E.
Gross,
A. van
der
Woude,
A. Zucker,
and
R.
H. Bassel,
to
be
published.
END TO
THE
COSMIC-RAY
SPECTRUM'~
Kenneth Greisen
Cornell
University, Ithaca,
New York
(Received
1
April
1966)
The
primary
cosmic-ray
spectrum
has been
measured
up
to
an
energy
of
10'
eV,
'
and
sev-
eral
groups
have
described
projects
under
de-
velopment
or in
mind'
to
investigate
the
spec-
trum
further,
into
the
energy
range
10"-10"
eV.
This note
predicts
that above
10'
eV
the
pri-
mary
spectrum
will
steepen
abruptly,
and
the
experiments
in
preparation
will at
last
observe
it
to
have
a
cosmologically
meaningful
termi.
-
nation.
The cause of
the
catastrophic
cutoff is
the
intense
isotropic
radiation first
detected
by
Penzias
and
Wilson'
at
4080
Mc/sec
(7.
35
cm)
and
now
confirmed as
thermal in
character
by
measurements of
Roll and
Wilkinson4
at
3.
2
cm wavelength.
It is not
essential
to the
pres-
ent
argument
that
the
origin
of this
radiation
conform
exactly
to the
primeval-fireball
mod-
el
outlined
by
Dicke,
Peebles,
Roll,
and
Vfil-
kinson',
what
matters
is
only
that
the
radia-
tion
exists and
pervades
the
observable
uni-
verse.
The
transparency
of
space
at
the
per-
tinent
wavelengths,
and
the
consistency
of
in-
tensity
observations in
numerous directions,
748
VOLUME
16,
NUMBER
17
PHYSICAL REVIEW LETTERS
25
APRIL
1966
give
strong
assurance
that the radiation is
in-
deed universal.
The
equivalent black-body
temperature has been
reported as
3.
1+
1'K'
and
3.
0+0.
5'K.
'
For our
discussion, we shall
consider
T
=3.
0,
at
which
temperature the
photon density
is 548
cm
'
and
the
mean
pho-
ton
energy
7.
0x10
4
eV.
Although
at
this
tem-
perature
the
number of
photons
in
the
spectral
range
of the measurements
(A
=-
3.
2
cm)
is
only
5
&10
'
of the
total,
the
slope
of
the
spec-
trum is such
that
any
reasonable
extrapola-
tion to
shorter
wavelengths
would
yield
at least
a
substantial
part
of
the
3'
black-body
photon
density. Moreover,
two
indirect
confirma-
tions of the existence
of the radiation
have been
reported:
One
lies in the
slope
of the
isotropic
part
of
the
x-
and
gamma-ray
spectrum'
and
the
other in the
absence
of muon-poor air
show-
ers
above
10"
eV.
'
As the last
statement
implies,
severa, l
con-
sequences
of the existence
of the
thermal
ra-
diation
have
quickly
been
noted. One is to pro-
vide
a
source
of
x
rays
and
gamma
rays
by
inverse
Compton
interactions with
cosmic-
ray
electrons.
'»
Another is
to make the
universe
opaque
to
high-energy
photons,
above
2
x10'4
eV,
because of positron-electron
pair
creation
by
photon-photon
interactions.
'~"
A
third effect is
to
deplete
the
density
of
en-
ergetic
electrons
by
the
energy
losses
in the
inverse
Compton
interactions.
'~'
Hoyle'
also
considered the effect of the
thermal radiation
on cosmic-ray
protons,
but concluded
that the
time scale
for
energy
degradation
is
greater
than
the
expansion
time
of the universe
for all
protons
up
to
10
'
eV. This
conclusion
is
wrong
because he
only
considered
the
proton
Comp-
ton
effect
and
neglected
two
stronger
proces-
ses, namely
pair
creation and
photopion
pro-
duction,
which we now wish
to examine.
The
threshold
energy
for
pion
production
by
protons
on
photons
of
energy
7
x10
~
eV
(the
mean
energy
of black-body radiation
at
3'K)
is
10'
eV,
and some
pion
production
occurs
at
lesser
proton
energies
because
of the
high-
frequency
tail
of the
photon
spectrum.
The
cross section rises
rapidly
above the
thresh-
old
p
going
through
a
peak
exc
ceding
400
p,
b
at
the
~„~
resonance
(2.
3
x10'0-eV
proton
en-
ergy
on
7
x10
'-eV
photon),
and descending
thereafter
to about
200
p.
b,
about which
mi-
nor
wiggles
occur
owing
to the
superposition
of
higher
resonances.
With
a
mean
cross
sec-
tion
of
200
pb
and
a
photon
density
of
550
cm
the
mean
path
for
interaction
is
(nv)
'
=9
x10'4
cm.
However,
the
distance
scale for
loss
of
energy
is
L
=(E/AE)(nv)
',
E
being
the initial
proton
energy
and AE
the
energy
loss
per
in-
teraction.
At the
threshold for
single-pion
production,
~/E
is
only
0.
13,
but
it
rises
to
an
average
value of 0.
22
at
the
-,
',
-,
reso-
nance,
and continues
to rise
thereafter
as
multiple
pions
are
produced
or more
kinetic
energy
is
given
to
a,
single
pion.
L
is
there-
fore on
the
order
of
4x10"
cm,
and the
time
sca.
le for
energy
loss is
10"
sec,
which
is
several
hundred times less
than
the
expansion
time
of
the universe.
L is also more
than
an
order
of
magnitude
less
than
the
distance to
the
nearest
quasar.
There
is
abundant
evidence
that
above
10"
eV,
the
cosmic
rays
are not confined
to
the
galaxy;
the
local
intensity
is
a
sample
of the
flux in
a
much
larger
sphere.
If
the sources
of
very
high-energy
particles
are
uniformly
distributed in
space
and
time,
the
effect of
interactions like those
described here is to
deplete
the
spectrum
by
a
factor
equal
to the
ratio of
the time
scale
for
energy
loss to
one-
third the expansion
time.
If,
on the other
hand,
the sources of such
particles
exist
only
far
back in time
or
at
great
distances,
the deple-
tion
is
much
stronger.
It
may
also be
noted
that
if
the
primeval-fireball model is
correct,
going
back
in
time
raises the mean
photon
en-
ergy
as
(1-t/T)
'
and
the
photon
density
as
(1
t/T),
T
bein—
g
the expansion
time;
thus
the effect
may
be
somewhat
larger
than
our
computations
on
a
static model
indicate.
It
should be noted that the cut in the
spectrum
due to
photopion
processes
is
rather
sharp,
because
of
the
steepness
of
the
high-frequency
tail
of
the
Planck distribution.
Only
1%
of
the
photons
have
energies
exceeding
3 times
the mean
value; also,
close to the
threshold
the cross section
is smaller than
200
p,
b and
the fractional
energy
loss
per
interaction
is
a
minimum. Therefore,
below
3
&10"
eV the
process
should have
a completely negligible
effect on the
proton
spectrum.
As
10'
eV is
approached,
the
effect should rise
rapidly',
and above
2
x
1
0
eVp
it
should be a, factor
of several hundred. At
present
the data
above
10'9
eV are rather
sparse,
and the
highest
energy
recorded is
represented
by
a single
event
at
10'0
eV.
'
A
smooth representation
and extrapolation
of
the spectrum
gives
an
integra,
l
frequency
of
about
one event on
100
VOLUME
16,
NUMBER
17
PHYSICAL
REVIEW LETTERS
2$
APRIL
1966
km'
in one
year
at energies
above
2
x10
eV.
If this number
is
cut
by
a
factor
of several
hundred, owing
to
the
y-p
reaction,
the
rate
will be far
too low to
be
detected
by
any
of
the
methods
yet
proposed;
even the
one event
recorded
at
10'
eV
appears
surprising.
One cannot
save
the
day
for
superhigh-en-
ergy
cosmic
rays
by
calling
on
heavy
nuclei.
The
threshold for
photodisintegration against
photons
of 7
&10
~
eV is
only
5x10'8
eV/nu-
cleon,
and
at
10"
eV/nucleon
most of
the
photons
can
excite the
giant
dipole
resonance,
for which the cross
section is on
the
order
of 10
"
cm'.
At this
energy
the
mean
path
for
photodisintegration
is
on
the order
of
2
x10
'
cm,
much
less than the
size of
the
gal-
axy.
Even nuclei 5
times less
energetic
would
be
decomposed
in
a
time
short
compared
with
the expansion
time of
the
universe, owing
to
the high-frequency
tail
of
the
black-body
spec-
trum.
Ordinary
optical
interstellar radiation can
also
produce
y-p
photopions
and
heavy
nucleus
disintegrations,
at
energies
1000 times
less
than
those
discussed
above;
but the intergalac-
tic
optical photon
density
is
smaller than
that
of the
3'
radiation
by
a
factor
of about 5x10,
and
the
mean
paths
are
correspondingly
longer.
So
the
effect on the
proton
spectrum
is
negli-
gible,
but
not the
effect
on
the
heavy
nuclei:
Above
10"
eV/nucleon
the mean time
for
pho-
todisintegration
is
an
order
of
magnitude
less
than the expansion
time.
Nuclei
confined in
the
galaxy
encounter
a higher density
of
optical
photons
and
are
fragmented
much
faster.
In
addition
to
photopion
interactions as
a
source
of
energy
loss to
high-energy protons,
one
should
consider
pair
production
by
the
thermal
photons.
The
proton
energy
threshold
for this
reaction
against
photons
of
7x10
eV
is
only
7
x10"
eV.
The
energy
loss in the
laboratory system
arises
primarily
from
the
small
longitudinal
momentum
given
to
the
pro-
ton
in its rest system.
At
the
threshold the
fractional
energy
loss
is
2m/M=10
',
where
m and
M
are the
electron
and proton
masses.
At
higher
energies
the
energy
loss
depends
on the
relative
velocity
of the
electron and
positron
and the
transverse
momentum
given
to the
proton,
but
the
average
energy
loss
in
the
laboratory
is
approximately
constant,
making
the
fractional
energy
loss
f
=
10 '/x,
where x
is
the ratio
of
the
proton
energy
to
its
threshold value. The cross section
with
no
screening is
approximately
1.
8X
10
27(lm
-0.
5)
cm'.
Therefore,
the scale
length
for
energy
loss is
given
by
L
=
(nfl)
'=
10
7
x
(1ruc
-0.
5)
'
cm. The
minimum
value of L occurs
at x
=4.
5 or
E
=3x10'
eV
and is
about
half
of
the Hubble
length. Thus,
the
effect
on
the
primary
spectrum
is
barely significant,
cre-
ating a
small
depression
(never exceeding
a
factor
of about
3)
in the interval
10"-10"
eV.
Even this small
depletion
of the flux
above
10"
eV,
however,
followed
above
5x10'9
eV
by
a
stronger depression
due to
the
photopion
process,
makes the
observed'
flattening
of
the
primary
spectrum
in the
range
10'
-10'
eV
quite
remarkable. The
injection spectrum
of
the
intergalactic
flux
must be much less
steep
than
that
of
the
galactic
particles
which
dominate
at
lower
energies.
The author
expresses
thanks
for
the hospi-
tality
of
the
Physics
Department
of the
Univer-
sity
of
Utah,
where
this
Letter
was written.
J.
Linsley,
Phys.
Rev. Letters
10,
146
(1963);
and
in
Proceedings
of the International
Conference on
Cos-
mic
Rays,
Jaipur
1963,
edited
by
R. R.
Daniel
et al.
(Commercial
Printing
Press,
Ltd.
,
Bombay,
India,
1964-1965),
Vol.
IV,
p,
77.
C.
B.
A.
McCusker and
K,
Greisen,
in
Proceedings
of
the International Conference
on
Cosmic
Rays,
Lon-
don,
September,
1965
(to
be
published);
and
S.
Col-
gate,
private
communication.
3A.
A.
Penzias and
R. W. Wilson,
Astrophys.
J.
142,
419
(1965).
4P.
G.
Roll and
D.
T.
Wilkinson,
Phys.
Rev. Letters
16,
405
(1966).
R.
H. Dicke, P.
J. E. Peebles,
P.
G. Roll,
and
D.
T.
Wilkinson,
Astrophys.
J.
142,
414
(1965).
8Private
communication from
Penzias and
Wilson,
reported
in
Ref.
4.
J.
E.
Felten,
Phys.
Rev. Letters
15,
1003
(1965).
R.
J.
Gould
and
G.
Schrbder,
Phys.
Rev. Letters
16,
253
(1966).
~F.
Hoyle, Phys.
Rev.
Letters
15,
131
(1965).
R.
J. Gould,
Phys.
Rev. Letters
15,
511
(1965)'.
~~J.
V.
Jelley, Phys.
Rev. Letters
16,
479
(1966).
R.
R.
Wilson,
Phys.
Rev.
110,
1212
(1958).
750
Particles having energies above $10^{18}$ eV are the so-called ultra-high-energy cosmic rays (UHECR). The UHECR are the most energetic particles known in the Universe.
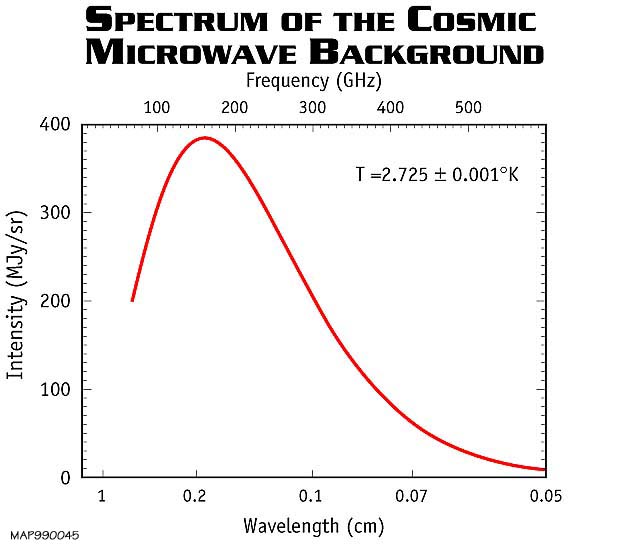
The Cosmic Microwave Background (CMB), discovered in 1966 by A. Penzias and R. Wilson, corresponds to the remnant photons of the Big Bang and acts like a black body spectrum with temperature T$_{\mathrm{CMB}} \simeq$ 2.73 K. At the highest energies, the Universe is no longer transparent to Cosmic Rays, that start interacting with the CMB photons.
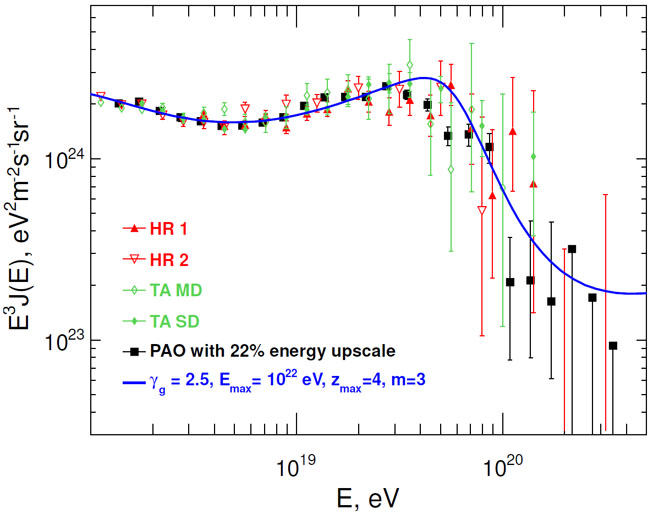
Spectrum of UHECR as observed by HiRes, TA and Auger experiments (as labeled). One can clearly observe a drop in the spectrum for Cosmic Ray energies above $10^{20}$ eV. K. Greisen's prediction was experimentally observed by three different experiments.
Today the upper limit on the energy of Cosmic Rays is called **Greisen–Zatsepin–Kuzmin limit (GZK limit)**. Several months later G. Zatsepin and V. A. Kuzmin published
[Upper Limit of the Spectrum of Cosmic Rays](http://www.jetpletters.ac.ru/ps/1624/article_24846.pdf).
The main reactions causing energy losses while the CR propagation are:
* Compton interactions of nuclei
* Pair production
* Photodisintegration of the nucleus
* Photopion production
In the case of UHECR the reaction that has the most influence on the spectrum is photopion production given by the following interactions:
\begin{eqnarray*}
p +\gamma_{\text{CMB}} &\longrightarrow& \Delta^+ \longrightarrow p + \pi_0\\
p +\gamma_{\text{CMB}} &\longrightarrow& \Delta^+ \longrightarrow n + \pi^+\\
p +\gamma_{\text{CMB}} &\longrightarrow& \Delta^{++} +\pi^- \longrightarrow p + \pi^+ + \pi^-\,\,
\end{eqnarray*}where $p$ is the UHECR and $\gamma_{\text{CMB}}$ are the CMB photons.
Spectrum of cosmic rays as a function of their energy given by several different experiments.

We can easily determine the distance scale for energy loss given by:\begin{eqnarray*}\lambda_{E}=\frac{1}{\kappa \rho_{\gamma} \sigma_{\text{p}\gamma}}\end{eqnarray*}where $\kappa$ is the inelasticity (fraction of the initial energy available for the production of new particles), $\rho_\gamma$ is the CMB photon density, and $\sigma_{\text{p}\gamma}$ is the mean p-$\gamma$ interaction cross section. Using these values we find that $\lambda_{E}\simeq 10^{25}\,\textrm{cm}\simeq 3.24\, \textrm{Mpc}$.
For each distance $\lambda_{E}$ the CR will loose 22% of its energy due to interactions with the CMB. The distance obtained corresponds to a characteristic time scale for energy loss of the order of $10^{15}$ s which is several orders of magnitude smaller than the age of the Universe ($4.3\times10^{17}$ s). This result could indicate that super GZK CRs:
* There are near sources that we have not identified yet. Protons arriving at Earth with super-GZK energies must come from sources situated at less than $\sim 100\,Mpc$ away.
* At the cutoff, the “visible” universe shrinks to a sphere of a few tens of Mpc of radius. This feature should be reflected in the energy spectrum of cosmic rays as a sharp drop.
As a simple exercise, one can calculate the threshold energy of protons (we consider the UHECR to be a proton) for the photopion production. It is easy to obtain the mean energy for the CMB. We know that the CMB has a temperature of $T_{\gamma} \simeq \, 2.73$ and a mean wavelength of $\lambda_{\gamma}= 1.96\,mm$, from which we can compute the mean energy as $E_{\gamma} = hc/\lambda_{\gamma} \simeq 6.34 \times 10^{-4} \, eV$.
Considering the proton and photon 4-momenta we have that the energy in the center of mass (CM) is given by:
\begin{eqnarray*}
\label{gzk1}
\left( p_{\text{p}} + p_{\gamma} \right)^{\mu}\left( p_{\text{p}} + p_{\gamma} \right)_{\mu} &=& m_{\text{p}}^2c^2 + 2\frac{E_{\text{p}}E_{\gamma}}{c^2}-2\vec{p}_{\text{p}}\cdot\vec{p}_{\gamma}
\end{eqnarray*}where $E_{\text{p}}$ is the energy, $m_{\text{p}}$ is the mass, and $\vec{p}_{\text{p}}$ is the three-dimensional momentum of the proton in the laboratory frame, and similarly for the photon. We can write the equation:\begin{eqnarray*}
\label{gzk2}
\left( p_{\text{p}} + p_{\gamma} \right)^{\mu}\left( p_{\text{p}} + p_{\gamma} \right)_{\mu} &=& m_{\text{p}}^2c^2 + 2\frac{E_{\text{p}}E_{\gamma}}{c^2} \left( 1- \cos{\theta} \right)
\end{eqnarray*}where we have used the fact that protons are ultrarelativistic so $\beta \approx 1$. To find the threshold energy of this reaction we use the above equations and we assume a frontal collision $\theta=\pi$. We know that the threshold energy in the center of mass for this reaction is given by $\sqrt{s}=\left(m_{\text{p}}+m_{\pi^0}\right)c$. Finally we have that the threshold energy for the protons is given by:\begin{eqnarray*}
\label{gzk3}
4\frac{E_{\text{p}}E_{\gamma}}{c^2} + m_{\text{p}}^2c^2 &=& \left( m_{\text{p}} + m_{\pi^0} \right)^2c^2
\end{eqnarray*}and the solution to of this equation for $E_{\text{p}}$ is:\begin{eqnarray*}
\label{gzk4}
E_{\text{p}} &=&\frac{m_{\pi^0}\left( 2m_{\text{p}} + m_{\pi^0} \right)c^4}{4E_{\gamma}}\,\,.
\end{eqnarray*}Using the mean energy for the CMB we find that $E_{\text{p}}\simeq 1.07\times 10^{20}$ eV.
We have found that protons with energies equal or higher than $10^{20}$ eV will interact with the CMB thus losing part of their energy.