Note that the author uses the identity $24 = 4(1+2+3)=4T_3$ to divide the square in 3 sections which he then uses as borders to augment the other squares: $21^2,22^2,23^2$ and turn them into $27^2,26^2,25^2$ He is telling you add the values to the original proposed formula: $$(k-1)^2 + k^2 = (k+1)^2 $$ Getting a new one, and then, you simplify that equation, and the recurrence you get is the one he's telling. In this paper Boardman gives us a visual motivation of why the relation of the "Pythagorean Runs" works. Here is another way to prove the same identity. Suppose we want to find 3 consecutive integers such that the sum of the squares of the first 2 is equal to the sum of the squares of the last. $$ (k-1)^2+k^2 = (k+1)^2 $$ If we expand the terms and simplify the equation we end up with $$ k^2-4k=0 $$ Now suppose we add $(k-2)^2$ to the left side and $(k+2)^2$ to the right side we end up with $$ k^2-4k-8k=0 $$ or $$ k^2-4k(1+2)=0 $$ In general if we add add $(k-n)^2$ to the left side and $(k+n)^2$ to the right side we will be adding an extra $-4kn$ to the equation. As a consequence $$ (k-n)^2+...+k^2 = (k+1)^2+...+(k+n)^2 $$ is equivalent to $$ k^2-4k\underbrace{(1+2+...+n)}_{T_n}=0 $$ This equation has 2 solutions: $k=0$ and $k=4T_n$. We conclude that apart from the trivial solution the only way to find $2n+1$ consecutive integers, such that the sum of the squares of the first $n+1$ is equal to the sum of the squares of the last $n$ is if $k=4T_n$! If we take some time to analyze these 3 equalities we can notice a pattern. To understand the pattern we should start by defining what a triangular number is. 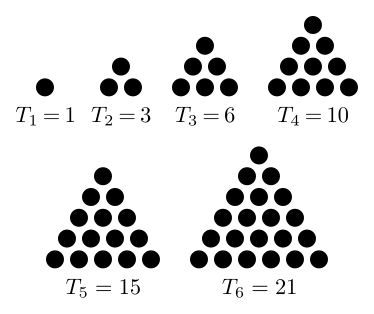Triangular numbers are numbers of the form: $$ T_n = 1+2+...+n $$ Which are visually represented as follows:  Now if we look at the number immediately to the left of the equal signs we see that it is the square of 4 times a triangular number: $$ 4 = 4(1) = 4T_1 \\ 12 = 4(1+2) = 4T_2 \\ 24 = 4(1+2+3) = 4T_3 $$ which leads to $$ (4T_n-n)^2+...+(4T_n)^2=(4T_n+1)^2+...+(4T_n+n)^2 $$ What's the reason for adding two different values to the different sides of the equation, wouldn't that change the equality of the equation? Michael Boardman is a mathematician at Johns Hopkins University whose speciality is algebraic and differential topology. Boardman is most widely known for his construction of the first rigorously correct model of the homotopy category of spectra.