Another interesting fact has to do with twin primes. A twin prime is a prime number that is either 2 less or 2 more than another prime number. Although no one was able to prove so far that there are infinitely many twin primes (the famous twin prime conjecture), in 1919 Viggo Brun proved the remarkable theorem that the sum of the reciprocals of the twin primes converges! The series of prime reciprocals is an old problem that was first solved by Euler in 1737. Euler showed that the divergence of the series implies Euclid's Theorem on the existence of infinite primes. To do so he used the product formula $$ \sum_{n=1}^{\infty}\frac{1}{n}= \prod_{p} \left( 1+\frac{1}{p}+\frac{1}{p^2}+\cdots \right) = \prod_{p} \frac{1}{1-p^{-1}} $$ If you want to learn more about Euler's proof click [here](https://en.wikipedia.org/wiki/Divergence_of_the_sum_of_the_reciprocals_of_the_primes). In this paper James Clarkson gets to the same result without making use of the uniqueness of factorization into primes nor the product formula; it just requires that every integer greater than 1 can be written as a product of primes. James Clarkson was an american number theorist. He is known for proving inequalities in Hölder spaces, and derived from them, the uniform convexity of LP spaces. He was also an operations' analyst during World War II, and was awarded the Medal of Freedom for his achievements. Note that $$ \sum_{i=1}^{r}\frac{1}{1+iQ} \leq \sum_{j=1}^{\infty}\left( \sum_{n=k+1}^{\infty}\frac{1}{p_n} \right)^j $$ since the right side includes among its terms all the terms on the left (every term $\frac{1}{1+iQ}$ can be written as a product $\frac{1}{p_a...p_b}$ where $p_a,...,p_b \in P(r)$, at the same time if we expand the binomial $(\frac{1}{p_{k+1}}+\frac{1}{p_{k+2}}+...)^j$ it will always include the term $\frac{1}{p_a...p_b}$). 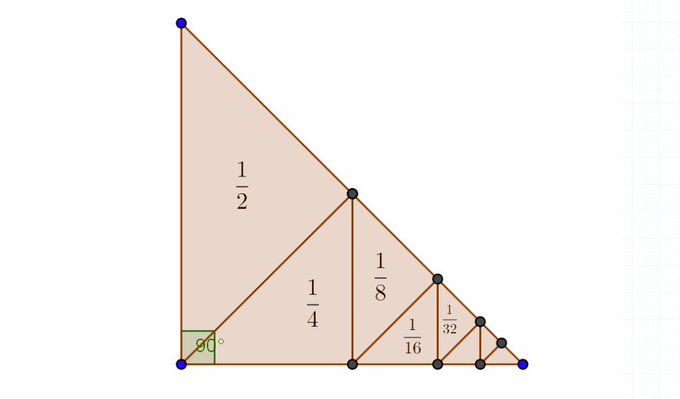Using the initial result $\sum_{n=k+1}^{\infty}\frac{1}{p_n}< \frac{1}{2}$ we end up with $$ \sum_{i=1}^{r}\frac{1}{1+iQ} \leq\sum_{j=1}^{\infty} \frac{1}{2^j} $$ The series $\sum_{j=1}^{\infty} \frac{1}{2^j}$ converges to 1 as we can conclude from the following image  This means $\sum_{i=1}^{\infty}\frac{1}{1+iQ}$ and consequently the harmonic series $\sum_{i=1}^{\infty}\frac{1}{i}$ converge which is a contradiction, since we know that $1+\frac{1}{2}+\frac{1}{3}+...=\infty$!